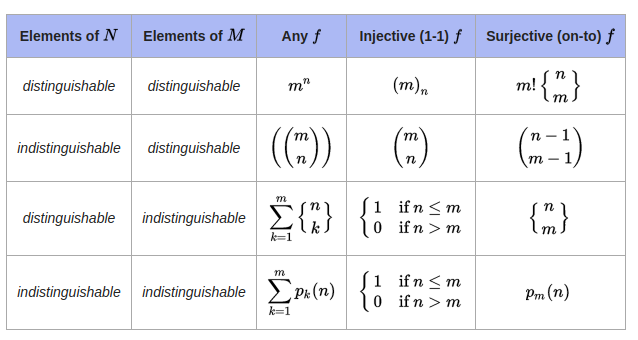
The twelvefold way
- $f: N\to M$, $|N|=n$, $|M|=m$
- 等价于

Basic Enumation
Tuples
$[m]=\\{0,1,2,\cdots, m-1\\}$
$n$-tuple of $[m]$: $[m]^n$
$|[m]^n|=m^n$, 可以通过The product rule严格证明
The product rule: 对于任意有限集$S$和$T$, $|S\times T|=|S|\cdot|T|$
Functions
考虑计算$[n]$到$[m]$的映射数问题.
- 等价于数$[m]$的$n$-tuple数
- 对于任意$f:[n]\to[n]$, 定义一个tuple$v_f\in [m]^n$, $v_f(i)=f(i-1)$, $i=1,2,\cdots, n$. 易证这是个双射.
- The bijection rule: 如果在有限集$|S|$和$|T|$之间存在双射, 则$|S|=|T|$
- 因此$[n]$到$[m]$的映射数等于$[m]^n$的tuple数, 即$m^n$
Subsets
数一个集合的子集数.
$S=\\{x_1,x_2,\cdots, x_n\\}$为$n$元集, $2^S=\\{T|T\subset 2^S\\}$为$S$所有子集的集合, 即$S$的幂集.
下证$|2^S|=2^n$:
每个$T\in 2^S$对应一个独特的位向量$v\in \\{0,1\\}^S$, $v_i$对应是否$x_i\in T$.
定义映射$\phi: 2^S\to \\{0,1\\}^n$, $\phi(T)=(v_1,v_2\cdots,v_n)$, 其中
易证$\phi$也是双射
因此$|2^S|=|\\{0,1\\}^n|=2^n$
证法2:
- 定义$f(n)=|2^{S_n}|$, $S_n=\\{x_1,x_2, \cdots, x_n\\}$.
- 证明$f(n)=2f(n-1)$. (分含不含$x_n$的情况)
- $f(0)=1$
- 因此$|2^S|=f(n)=2^n$
Subsets of fixed size
某集合的固定大小的子集的数量
- 定义$\left(\begin{array}{cc} S \\\\k \end{array}\right)$为$S$的$k$元子集. $\left(\begin{array}{cc} S \\\\k \end{array}\right)=\\{T\subseteq S||T|=k\\}$. $\left(\begin{array}{cc} n \\\\k \end{array}\right)=\left|\left(\begin{array}{cc} S \\\\k \end{array}\right)\right|$, 读作”n选k”
- 定理: $\left(\begin{array}{cc} n \\\\k \end{array}\right)=\frac{n(n-1)\cdots(n-k+1)}{k(k-1)\cdots 1}=\frac{n!}{k!(n-k)!}$, 常记做$(n)_k$
Binomial coefficient
- $\left(\begin{array}{cc} n \\\\k \end{array}\right)=\left(\begin{array}{cc} n \\\\n-k \end{array}\right)$
$\sum_{k=0}^n \left(\begin{array}{cc} n \\\\k \end{array}\right)=2^n$
二项式定理: $(1+x)^n=\sum_{k=0}^n \left(\begin{array}{cc} n \\\\k \end{array}\right)x^k$
推论: $n$元集的奇数势子集和偶数势子集数量相同
Compositions of an integer
$n$的composition为将$n$表示为有序的正整数的和. $n$的$k$-composition是将$n$表示为$k$个有序的正整数的和
形式化地, $n$的$k$-composition是一个$k$-tuple$(a_1,a_2,\cdots,a_k)\in\\{1,2,\cdots,n\\}^k$, 满足$a_1+a_2+\cdots +a_k=n$.
根据隔板法(略), $n$的$k$-composition数为$\left(\begin{array}{cc} n -1 \\\\k -1\end{array}\right)$
严格证明: 构建$n$的$k$-composition和$\left(\begin{array}{cc} \\{1,2,\cdots, n-1\\} \\\\k-1 \end{array}\right)$之间的双射:
- $\phi((a_1,a_2,\cdots,a_k))=\\{a_1,a_1+a_2,\cdots, a_1+a_2+\cdots+a_{k-1}\\}=\\{\sum_{i=1}^ja_i|1\le j<k \\}$
- 将每个$k$-composition映射到$\\{1,2,\cdots,n-1\\}$的一个$(k-1)$子集, 易证为双射, 得证.
$n$的$k$-composition等价于$x_1+x_2+\cdots+x_k=n$的正整数解的数量, 而$x_1+x_2+\cdots+x_k=n$的非负整数解称作$n$的弱$k$-composition.
- $n$的弱$k$-composition是tuple$(x_1,x_2,\cdots,x_k)\in [n+1]^k$满足$x_1+x_2+\cdots+x_k=n$
- 对于一个$n$的弱$k$-composition$(x_1,x_2,\cdots, x_k)$, 我们定义$y_i=x_i+1>0$, 则$y_1+y_2+\cdots+y_k=n+k$, $(y_1,y_2,\cdots,y_k)$是$n+k$的$k$-composition.
- 因此$n$的弱$k$-composition数为$\left(\begin{array}{cc} n+k -1 \\\\k -1\end{array}\right)$
下面数$x_1+x_2+\cdots+x_k\le n$的非负整数解.
- 令$x_{k+1}=n-(x_1+x_2+\cdots+x_k)\ge 0$. 因此$x_1+x_2+\cdots+x_{k+1}=n$.
- 问题转化为上式的非负整数解的数量. 答案是$\left(\begin{array}{cc} n + k \\\\k\end{array}\right)$
Multisets
- $n$的$k$子集也称为$k$-combination of $S$ without repetitions. 下面考虑$k$-combination of $S$ with repetitions. 也就是我们选择$S$中的$k$元素, 不管顺序, 允许重复. 也称为multisets.
- 形式化地, 考虑映射$m: S\to \mathbb N$. 对于任意$x\in S$, $m(x)\ge 0$是$x$在$M$中的重复次数, 称为multiplicity. $|M|=\sum_{x\in S}m(x)$称为$M$的势. $k$-multiset满足$|M|=k$
$S$的$k$-multisets表示为$\left(\left(\begin{array}{cc} S \\\\k \end{array}\right)\right)$. 记$n=|S|$, 表示$\left(\left(\begin{array}{cc} n \\\\k \end{array}\right)\right)=\left|\left(\left(\begin{array}{cc} S \\\\k \end{array}\right)\right)\right|$
$\left(\left(\begin{array}{cc} n \\\\k \end{array}\right)\right)=\left(\begin{array}{cc} n+k-1 \\\\n-1\end{array}\right)=\left(\begin{array}{cc} n+k-1 \\\\k\end{array}\right)$, 因为其实就是$m(x_1)+m(x_2)+\cdots+m(x_n)=k$的解的数量
- 直观解释:
- 给定一个$[n]$上的$k$-multiset $0\le a_0\le a_1 \le \cdots \le a_{k-1}\le n-1$, 定义$b_i=a_i+i$, 则$\\{b_0,b_1,\cdots,b_{k-1}\\}$是$[n+k-1]$的$k$-subset. 同样的, 给定$b_i$满足$0\le b_0\le b_1\le \cdots b_{k-1}\le n+k-2$, 也能定义对应的$a_i=b_i-i$, $\\{a_0,a_1,\cdots.a_{k-1}\\}$是$[n]$上的$k$-multiset. 因此就有了$\left(\left(\begin{array}{cc} [n] \\\\k \end{array}\right)\right)$到$\left(\begin{array}{cc} [n+k-1] \\\\k \end{array}\right)$的双射.
Multinomial coefficients
$\left(\begin{array}{cc} n \\\\k \end{array}\right)$理解为将$n$个元素分成两组, $k$个在第一组, 剩下的在第二组, 即下面说的$\left(\begin{array}{cc} n \\\\k,n-k \end{array}\right)$
$(a_1,a_2,\cdots, a_m)$为和为$n$的非负tuple. $\left(\begin{array}{cc} n \\\\a_1,a_2 ,\cdots, a_m\end{array}\right)$为把$n$元集的每个元素配分到$m$个组$G_1,G_2\cdots,G_m$之一的种数, 称为多项式系数. 也可以理解为$n$个标记了的球分配到$m$个标记了的箱子, 第$i$个箱子有$a_i$个球的种数
还可以被理解为multiset的排列数. $n$元集$S$的排列$\pi$可以用一下两种等价方法定义:
- 双射$\pi: S\to S$
- tuple $\pi=(x_1,x_2,\cdots,x_n)\in S^n$, $x_i$不同
$n$元集有$n!$中排列
A permutation of a multiset$M$是一个tuple $\pi=(x_1,x_2,\cdots,x_n)$满足$x_i\in M$出现$m(x_i)$次
例子: 某个单词重排的种数
因此$\left(\begin{array}{cc} n \\\\a_1,a_2 ,\cdots, a_m\end{array}\right)$也是multiset$M$的排列数, 其中$|M|=n$.
$\left(\begin{array}{cc} n \\\\a_1,a_2 ,\cdots, a_m\end{array}\right)$是$(x_1+x_2+\cdots+x_m)^n$中$x_1^{a_1}x_2^{a_2}\cdots x_m^{a_m}$的系数
- 证明: $n$因子中任意一个对应一个不同的球, $x_1,x_2,\cdots,x_m$对应$m$个组, $x_1^{a_1}x_2^{a_2}\cdots x_m^{a_m}$的系数等于把$n$个球放入$m$个不同的箱子, 其中第$i$个箱子有$x_i$个球, 也就是上面的式子.
Partitions of a set
有限集$S$的划分Partition是collection$P=\\{S_1,S_2,\cdots,S_k\\}$, 为$S$的子集, 满足
- 对任意$i$, $S_i\ne\emptyset$
- 任意$i\ne j$, $S_i\cap S_j=\emptyset$
- $S_1\cup S_2\cup \cdots S_k=S$
每个$S_i$称为划分$P$的一个块block. $P$是$k$-partition如果$|P|=k$
定义$\left\\{\begin{array}{cc} n \\\\k\end{array}\right\\}$为$n$元集的$k$划分数量. 注意我们并不关心$S_1,S_2,\cdots,S_k$的顺序. 也称为第二型斯特林数
递归式
- 证明时分两类:
- $n$单独一个块
- $n$非单独一块
- 证明时分两类:
定义$B_n=\sum_{k=1}^n\left\\{\begin{array}{cc} n \\\\k\end{array}\right\\}$. 称作Bell数
Partitions of a number
数$n$相同元素分到$k$无序集合的数量, 等价于数把数$n$划分到$k$个无序部分的种类
$n$的$k$划分是multiset$\\{x_1,x_2,\cdots,x_k\\}$满足$x_i\ge 1$, 且$x_1+x_2+\cdots+x_k=n$, 其数量定义为$p_k(n)$
等价地, 我们可以定义其为$k$-tuple $(x_1,x_2,\cdots,x_k)$满足
- $x_1\ge x_2\ge \cdots \ge x_k\ge 1$
- $x_1+x_2+\cdots+x_k=n$
其数量为$p_k(n)$
$p(n)=\sum_{i=1}^n p_k(n)$是$n$的所有分割数, 称为partition number.
- 证明不妨设$x_1\ge x_2\ge \cdots \ge x_k\ge 1$
- 分成$x_k=1$和$x_k>1$两种
定理:
证明
- 考虑$(x_1,x_2,\cdots, x_k)$为$n$的$k$-Partition. 则$x_1+x_2+\cdots+x_k=n$, $x_1\ge x_2\ge \cdots x_k\ge 1$
- 因为每个$n$的$k$-composition都对应至少一个$(x_1,x_2,\cdots, x_k)$的$k!$个排列
- $n$的$k$-composition有$\left(\begin{array}{cc} n -1 \\\\ k -1\end{array}\right)$个
- 所以$k!p_k(n)\ge \left(\begin{array}{cc} n -1 \\\\k -1\end{array}\right)$
- 令$y_i=x_i+k-i$, 则一定有
- $y_1 > y_2 > \cdots > y_k \ge 1$
- $y_1+y_2+\cdots+ y_k=n+\frac{k(k-1)}{2}$
- $(y_1,y_2,\cdots,y_k)$的每个排列都落在不同的$n+\frac{k(k-1)}{2}$的$k$排列中, 因为所有的$y_i$都是不同的
- 因此$k!p_k(n)\le \left(\begin{array}{cc} n+\frac{k(k-1)}{2} -1 \\\\k -1\end{array}\right)$
- 综上$\frac{\left(\begin{array}{cc} n -1 \\\\k -1\end{array}\right)}{k!}\le p_k(n)\le \frac{\left(\begin{array}{cc} n+\frac{k(k-1)}{2} -1 \\\\k -1\end{array}\right)}{k!}$
Ferrers diagram
- 数字$n$的partition可以用Ferrers图表示. $(x_1,x_2,\cdots,x_k)$, $x_1\ge x_2 \ge \cdots \ge x_k\ge 1$是$n$的一个划分. 则对应的Ferrers图有$k$行, 第$i$行包含$x_i$个点(或方块). 如下图

对偶划分: 把Ferrers图的行和列交换, 如下图:
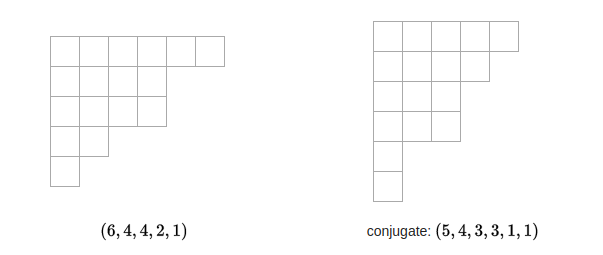
显然:
- 不同划分的对偶不同
- 每个划分都有对偶
命题:
$n$的每份至多为$k$的划分数为$p_k(n)$
- 因为对于每个$k$-partition都有对应的每份至多为$k$的对偶partition, 反之亦然.
$n$划分成$k$份的种数等于把$n-k$划分成至多$n-k$份的种数, 即
- Ferrers图去掉左边一列