Concentration of measure
1 Chernoff Bound
矩生成函数: 随机变量$X$的矩生成函数为
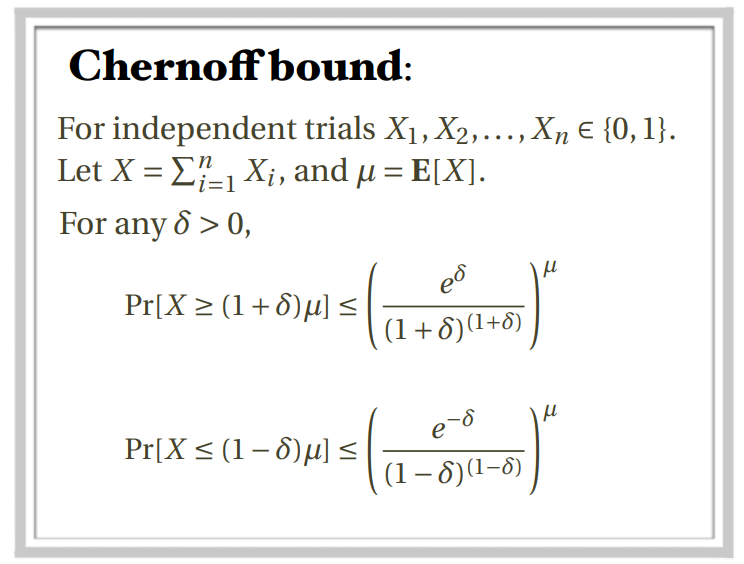
- 推导过程:
- $\Pr[X\ge (1+\delta)\mu]=\Pr[e^{\lambda X}\ge e^{\lambda(1+\delta)\mu}]\le \frac{\mathbb E[e^{\lambda X}]}{e^{\lambda X(1+\delta)\mu}}$
- $\mathbb E[e^{\lambda X}]=\mathbb E[e^{\lambda \sum_{i=1}^n X_i}]=\mathbb E[\prod_{i=1}^ne^{\lambda X_i}]=\prod_{i=1}^n\mathbb E[e^{\lambda X_i}]$
- $\mu=\mathbb E[X]=\sum_{i=1}^n \mathbb E[X]=\sum_{i=1}^np_i$
- $\mathbb E[e^{\lambda X_i}]=p_ie^\lambda +(1-p_i)e^0=1+p_i(e^\lambda -1)\le e^{p_i(e^\lambda-1)}$
- 合起来就得证
- 特例:
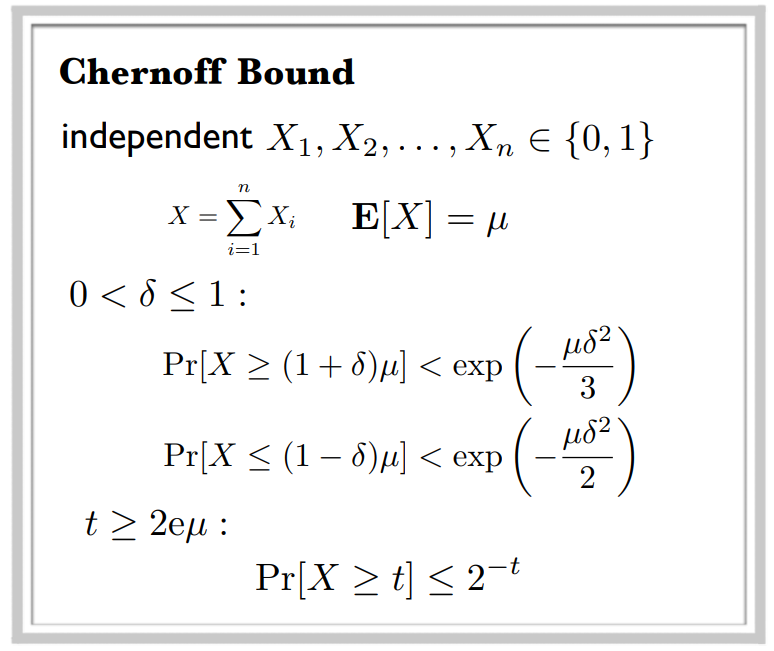
Balls into bins问题应用
计算w.h.p的最大装载:
$X_{ij}$表示第$i$ 个球是否扔进第$j$ 个箱子, 则$\mathbb E[X_{ij}]=1/n$.
令$Y_i=\sum_{j\in [m]}X_{ij}$表示箱子$i$ 的装载, 则$\mu=\mathbb E[Y_i]=\mathbb E[\sum\limits_{j\in [m]}X_{ij}]=\sum\limits_{j\in [m]}\mathbb E[X_{ij}]=m/n$.
The $m = n$ Case
在$m=n$时, $\mu=1$, $Pr[Y_i>(1+\delta)\mu]\le \left(\frac{e^\delta}{(1+\delta)^{1+\delta}}\right)^\mu$
令$c=\frac{e\ln n}{\ln \ln n}$, 则$ Pr[Y_i>c]\le \frac{e^{c-1}}{c^c}\le 1/n^2$
存在一个箱子装载大于$c$的概率小于等于$nPr[Y_1>c]\le 1/n$.
因此$m=n$时, 大概率最大装载为$O(\frac{e\ln n}{\ln \ln n})$
The $m>\ln n$ Case
类似方法得到: 大概率最大装载为$O(\frac{m}{n})$
2 Hoeffding Bound

证明用到:

推广:

Occupancy Problem应用
问题: $f:[m]\to [n]$, 求$f^{-1}(i)$为空的$i\in[n]$的数量.
$X_i$: 第$i $个箱子是否为空. $\mathbb E[X_i]=(1-1/n)^m$
$X=\sum_{i=1}^n X_i$: 空箱子数量. $\mathbb E[X]=n(1-1/n)^m$
$Y_j\in[n]$表示第$j$个球扔进的箱子号, 则$X$是$Y_1,\cdots, Y_n$的函数.
改变一个$Y_i$, $X$至多变化1.
应用bounded differences, 有$Pr[|X-n(1-1/n)^m]\ge t\sqrt m]=Pr[|X-\mathbb E[X]|\ge t\sqrt m]\le 2e^{-t^2/2}$
因此$m$和$n$较大时, 空箱子的数量大致集中于$n(1-1/n)^m\approx \frac{n}{e^{m/n}}$
Pattern Matching应用
问题: 字母表$|\Sigma|=m$, 长度为$n$的随机字符串, 长度为$k$的pattern, 求匹配子列数量$Y$.
$\mathbb E[Y]=(n-k+1)(\frac{1}{m})^k$(考虑匹配的字符串开始的位置)
原字符串$X_1,X_2,\cdots, X_n\in \Sigma$
$Y=f(X_1,X_2,\cdots, X_n)$, 改变$X_i$至多$Y$至多影响$k$, 因此
Combining unit vectors应用
问题: $u_1,u_2,\cdots,u_n$为$n$个正交空间中的单位向量. 独立均匀随机选取$\epsilon_1,\cdots, \epsilon_n\in \{+1,-1\}$ . 令$v=\epsilon_1 u_1+\cdots+\epsilon_n u_n$, 而$X=||v||$. 考虑$X$的分布.
$X$是独立随机变量$\epsilon_1,\cdots,\epsilon_n$的函数. 根据三角不等式, 改变一个$\epsilon_i$, $X$至多变化2. 因此
The Bounded Difference Method证明见讲义.