存在性问题
1 Existence by counting
1.1 Shannon’s circuit lower bound
布尔电路问题: $f:\{0,1\}^n\to \{0,1\}$, 三种门: AND, OR, NOT. 电路复杂度: 门的个数.
定理(Shannon):
存在布尔函数$f:\{0,1\}^n\to \{0,1\}$, 电路复杂度$>\frac{2^n}{3n}$.
证明:
$f:\{0,1\}^n\to \{0,1\}$的布尔函数个数: $2^{2^n}$.
数$t$个门的电路:
- 用De Morgan定律可以把所有的非门放在输入处, 这样以后每个门有两种(AND, OR), 都是2输入的.
- 门的每个输入都是0, 1, $x_i$, $\neg x_i$, 或者其他门的输入. 所以最多有$2+2n+t-1$个可能的门输入
- 因此$t$个门的电路数量至多为$2^t(2+2n+t-1)^{2t}$. (因为每个门有2种选择, 2个输入各有至多$2+2n+t-1$种选择)
- 如果$t=2^n/3n$, 则$\frac{2^t(2+2n+t-1)^{2t}}{2^{2^n}}=o(1)<1$, 因此$2^t(2+2n+t-1)^{2t}<2^{2^n}$.
- 所以有不能用$2^n/3n$个门计算的电路.
1.2 Double counting
1.2.1 Handshaking lamma
| Handshaking Lemma |
|---|
| At a party, the number of guests who shake hands an odd number of times is even. |
将握手看做图中的边, 则可以由一下引理得到:
| Lemma (Euler 1736) | ||
|---|---|---|
| $\sum_{v\in V}d(v)=2 | E | $ |
为了证明这个引理, 我们需要数有向边的数量:
- 每条边$uv\in E$有两个方向$(u,v)$和$(v,u)$, 所以有$2|E|$条有向边.
- 对于每个点$v\in V$, 有$d(v)$个邻居, 也就有$d(v)$条有向边$(v,u)$. 因此总共$\sum_{v\in V}d(v)$条有向边.
1.2.2 Sperner’s lemma
| Sperner’s Lemma (1928) |
|---|
| For any properly colored triangulation, there exists a cell receiving all three colors. |
properly coloring:
- 三个顶点a, b, c是三种不同的颜色
- 边ab, ac, bc上的点有两种颜色
证明:
如下构造对偶图:
- 每个cell看做一个点, 外围空间也看做一个点
- 对偶图中两点之间有边当且仅当原图中的这两个cell之间有红蓝边
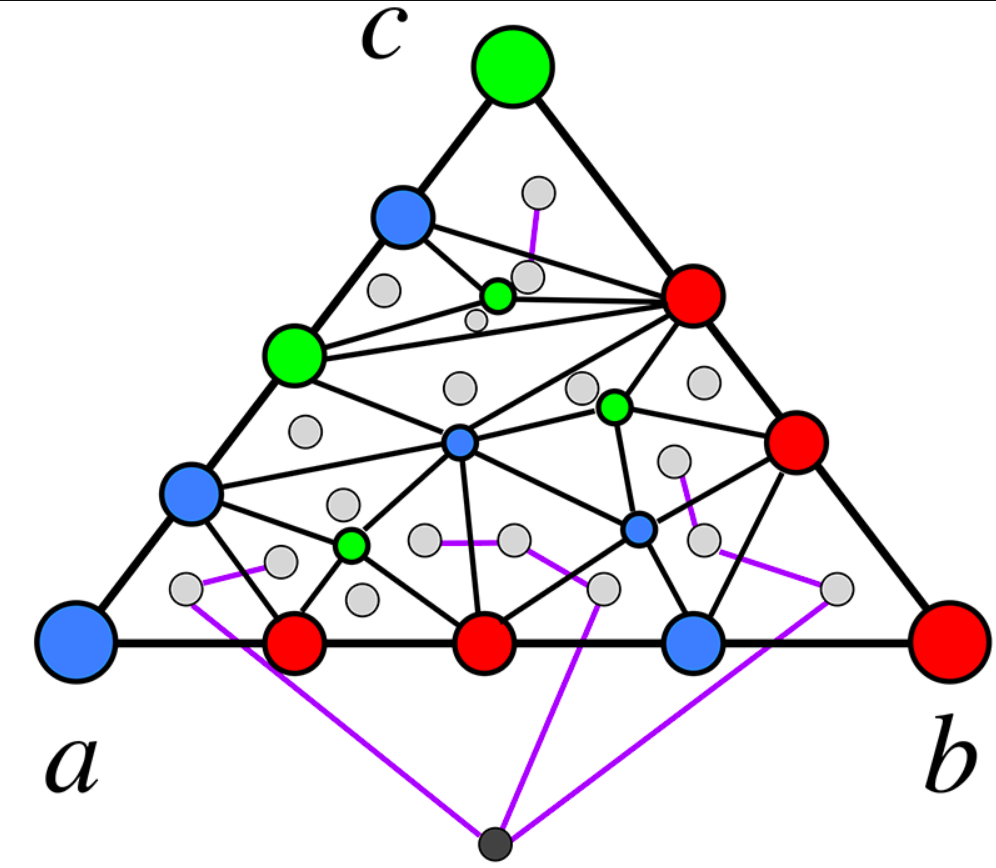
对于对偶图中的点:
- 如果原图中的cell有三色, 那么对偶图中对应点度为1
- 如果原图中的cell只有红蓝2色, 那么对偶图中对应点度为2
- 对于其他cell, 对偶图中对应点度为0
- 原图中外围空间对应的对偶图中点的度为奇数
根据handshaking lemma, 奇度点的个数为偶数, 因此原图中三色cell的数量为奇数, 非0.
2 The pigeonhole Principle
| Generalized pigeonhole principle |
|---|
| If a set consisting of more than $mn$ objects is partitioned into $n$ classes, then some class receives more than $m$ objects. |
2.1 Inevitable divisors
Theorem:
For any subset $S\subseteq \{1,2,\cdots,2n\}$ of size $|S|>n$, there are two numbers $a,b\in S$ such that $a|b$.
证明:
对于每个奇数$m\in \{1,2,\cdots,2n\}$, 令
显然同一类$C_m$中的两个数$b<a$一定有$a|b$.
而每个$a\in S$可以唯一表示为$a=2^km$其中$m$为奇数, 所以属于恰好一个类$C_m$, $m\in \{1,2,\cdots,2n\}$.总共$n$个奇数, 所以有$n$个不同的类$C_m$, 但是$|S|>n$, 所以一定有不同的$a, b\in S$在同一个类$C_m$, 不妨设$a>b$,则$a|b$ .
2.2 Monotonic sbusequences
| Theorem(Erdős-Szekeres 1935) |
|---|
| 一个长度大于$mn$的不同实数序列, 一定包含一个长度$m+1$的递增子列或者长度$n+1$的递减子列. |
设原序列为$(a_1,\cdots,a_N)$, $N>mn$, $a_i$为各不相同的实数.
对于$a_i$定义数对$(x_i,y_i)$如下:
- $x_i$: 最长的结束于$a_i$的递增序列的长度
- $y_i$: 最长的开始于$a_i$的递减序列的长度
- 下证只要$i\ne j$就有$(x_i,y_i)\ne(x_j,y_j)$: (不妨设$i<j$)
- 情形1: $a_i<a_j$, 则结束于$a_i$的递增序列可以加上$a_j$后仍然递增, 所以$x_i<x_j$.
- 情形2: $a_i>a_j$, 同理, $y_i>y_j$
- 因此我们把$N$个鸽子放在$\{1,2,\cdots,N\}\times \{1,2,\cdots,N\}$的笼子中, $a_i$放在$(x_i,y_i)$, 每个笼子至多一个鸽子.
- 因为$N>mn$, 所以一定有鸽子在$\{1,2,\cdots,m\}\times \{1,2,\cdots,n\}$以外的笼子内, 也就是$x_i>m$或$y_i>n$. 得证.
2.3 Dirichlet’s approximation
Theorem:
令$x$为一个无理数. 对于任意自然数$n$, 存在一个有理数$\frac{p}{q}$满足$1\le q\le n$且$|x-\frac{p}{q}|<\frac{1}{nq}$.
证明:
令$\{x\}=x-\lfloor x\rfloor$表示实数$x$的小数部分. 显然$\{x\}\in\{0,1\}$.
考虑$n+1$个数$\{kx\}$, $k=1,2,\cdots,n+1$. 这$n+1$个数字(鸽子)属于$n$个区间(笼子): $(0,1/n),(1/n,2/n),\cdots,((n-1)/n,1)$. 且因为$x$是无理数, 所以$\{kx\}$都不在区间两端.
根据鸽笼原理, 存在$1\le a\le b\le n+1$, 满足$\{ax\}$和$\{bx\}$在同一个区间, 因此有
因此
令$q=b-a$, $p=\lfloor bx\rfloor -\lfloor ax\rfloor$, 则$|qx-p|<1/n$且$1\le q\le n$.两边除以$q$, 得证.