极值图论

1 Fobidden Cliques

研究问题: 如果$G$满足某些性质, 那么$G$至多有多少条边?

1.1 Mantel’s theorem

定理(Mantel 1907):

假设$G(V,E)$ 是无三角形的$n$点图, 那么 $|E|\le n^2/4$.

证明1(鸽笼原理):

对$n$数归证明任意$G(V,E)$满足$|V|=n$且$|E|>\frac{n^2}{4}$一定有三角形:

$n\le 3$显然.
假设$|V|\le n-1$成立, 对于$n$点的图$G$, 不失一般性, 假设$|E|=\frac{n^2}{4}+1$. 对于任意$uv\in E$, 令$H$为$G$的$V\setminus\{u,v\}$的诱导子图. 显然$H$有$n-2$点.
1. 如果$H$有$>\frac{(n-2)^2}{4}$条边, 那么根据假设, $H$有三角形
2. 如果$H$有$\le \frac{(n-2)^2}{4}$条边, 那么$H$和$\{u,v\}$之间至少$(\frac{n^2}{4}+1)-\frac{(n-2)^2}{4}-1=n-1$条边. 根据鸽笼原理, $H$中一定有一个点和$u,v$都相邻, 所以$G$有三角形.

证明2(Cauchy-Schwarz inequality):

对于任意边$uv\in E$, 因为无三角形, 所以$d_v+d_u\le n$, 所以$\sum_{uv\in E}(d_u+d_v)\le n|E|$.
注意到$d(v)$在求和中出现了正好$d_v$次, 所以$\sum_{uv\in E}(d_u+d_v)=\sum_{v\in V}d_v^2$.
应用Cauchy-Schwarz inequality,

$n|E|\ge \sum_{uv\in E}(d_u+d_v)=\sum_{v\in V}d_v^2\ge \frac{(\sum_{v\in V}d_v)^2}{n}=\frac{4|E|^2}{n}$

其中最后一步使用了欧拉不等式(handshaking)$\sum_{v\in V}d_v=2|E|$.

证明3(inequality of the arithmetic and geometric mean):

$A$为$G$中最大的点独立集(两两不相邻的点的集合), 设$|A|=\alpha$. 因为$G$是无三角形的, 所以对于任意点$v$, 所有它的邻居必须形成一个独立集, 因此对于所有的$v\in V$, 有$d(v)\le \alpha$.
记$B=V\setminus A$, $\beta = |B|$. 因为$A$是点独立集, 所以所有$E$中的边至少有一个顶点在$B$中, 所以$|E|\le \sum_{v\in B}d_v$. 根据算数平均值和几何平均值的关系,

$|E|\le \sum_{v\in B}d_v\le \alpha\beta\le (\frac{\alpha+\beta}{2})^2=\frac{n^2}{2}$

1.2 Turan’s theorem

Turan’s theorem将Mantel’s theorem中的三角形团块推广到了任意特定的大小.
团块: 所有的点两两相邻.

定理(Turán 1941)

令$G(V,E)$为一个$|V|=n$的图. 如果$G$没有$r$团块, 则$|E|\le \frac{r-2}{2(r-1)}n^2$

无$K_r$图的例子: $K_{n_1,n_2,\cdots,n_{r-1}}$. (因为不同部分的点才能相邻)
定义: 完全多部图$K_{n_1,\cdots,n_{r-1}}$,对于任意$i$, $n_i\in\{\lfloor n/(r-1)\rfloor ,\lceil n/(r-1)\rceil\}$, 则称为Turán graph$T(n,r-1)$.

证明1(数归):

$n<r$显然.
假设$n<N$成立, 对于$n=N$, 假设$G$是最大$K_r$-free的, 也就是存在$r-1$团块, 记为$A$, 剩下的记为$B$. 因为假设, $|E(B)|\le \frac{r-2}{2(r-1)}(n-r+1)^2$. 又因为$K_r$-free, $B$中的点不可能和所有$v\in A$都相邻, 所以$E(A,B)\le (r-2)(n-r+1)$. $\begin{aligned} |E|&=|E(A)|+|E(A,B)|+|E(B)|\\ &\le \binom{r-1}{2}+\frac{r-2}{2(r-1)}(n-r+1)^2\le (r-2)(n-r+1) =\frac{r-2}{2(r-1)}n^2 \end{aligned}$

证明2(weight shifting):

分配给每个点$v$一个权重$w_v\ge 0$, $\sum_{v\in V}w_v=1$. 评估$S=\sum_{uv\in E}w_uw_v$.
令$W_u=\sum_{v:v\sim u}w_v$, 则$S=\frac{1}{2}\sum_{u\in V}w_uW_u$. 对于$u\not\sim v$满足$W_u\ge W_v$, 有$(w_u+\epsilon)W_u+(w_v-\epsilon)W_v\ge w_uW_u+w_vW_v$.
把所有的权重从$v$移动到$u$, $S$一定不减, 所以$S$最大—> 所有权重都在一个团块上.
因此$S=\sum_{uv\in E}w_uw_v\le \binom{r-1}{2}\frac{1}{(r-1)^2}$, 而当$w_i=1/n$时, $S=\sum_{uv\in E}w_uw_v=\frac{|E|}{n^2}$, 化简得证.

证明3(概率法):

$V=\{v_1,\cdots, v_n\}$, $d_i=d(v_i)$, 团块数$w(G)$: 最大的团块的大小.
证明$w(G)\ge \sum_{v\in V}\frac{1}{n-d_v}$:
随机排列$\pi$, 根据$\pi$中顺序将点加入$S$, $v_i$加入$S$如果$v_i$和所有$S$中现有的点都相邻.
令$X_v$表示$v$是否在$S$中. 如果所有$n-d_v-1$个顶点都排在它后面, 那么一定有$v\in S$, 这样的概率为$\frac{1}{n-d_v}$. 因此

$\mathbb E[X_v]=\Pr[v\in S]\ge \frac{1}{n-d_v}$

观察到$|S|=\sum_{v\in V}X_v$. 因为期望的线性, 有

$\mathbb E[|S|]=\sum_{v\in V}\mathbb E[X_v]\ge \sum_{v\in V}\frac{1}{n-d_v}$

因此肯定存在团块大小至少为这么多, 也就是$w(G)\ge \sum_{v\in V}\frac{1}{n-d_v}$.
接下来应用Cauchy-Schwarz不等式,

$(\sum_{v\in V}a_vb_v)^2\le (\sum_{v\in V}a_v^2)(\sum_{v\in V}b_v^2)$

设$a_v=\sqrt{n-d_v}$, $b_v=\frac{1}{\sqrt{n-d_v}}$, 则

$n^2\le \sum_{v\in V}(n-d_v)\sum_{v\in V}\frac{1}{n-d_v}\le w(G)\sum_{v\in V}(n-d_v)$

应用Turán’s theorem假设, $w(G)\le r-1$, 考虑到$2|E|=\sum_{v\in V}d_v$:

$n^2\le (r-1)(n^2-2|E|)$

化简即得证.

证明4:

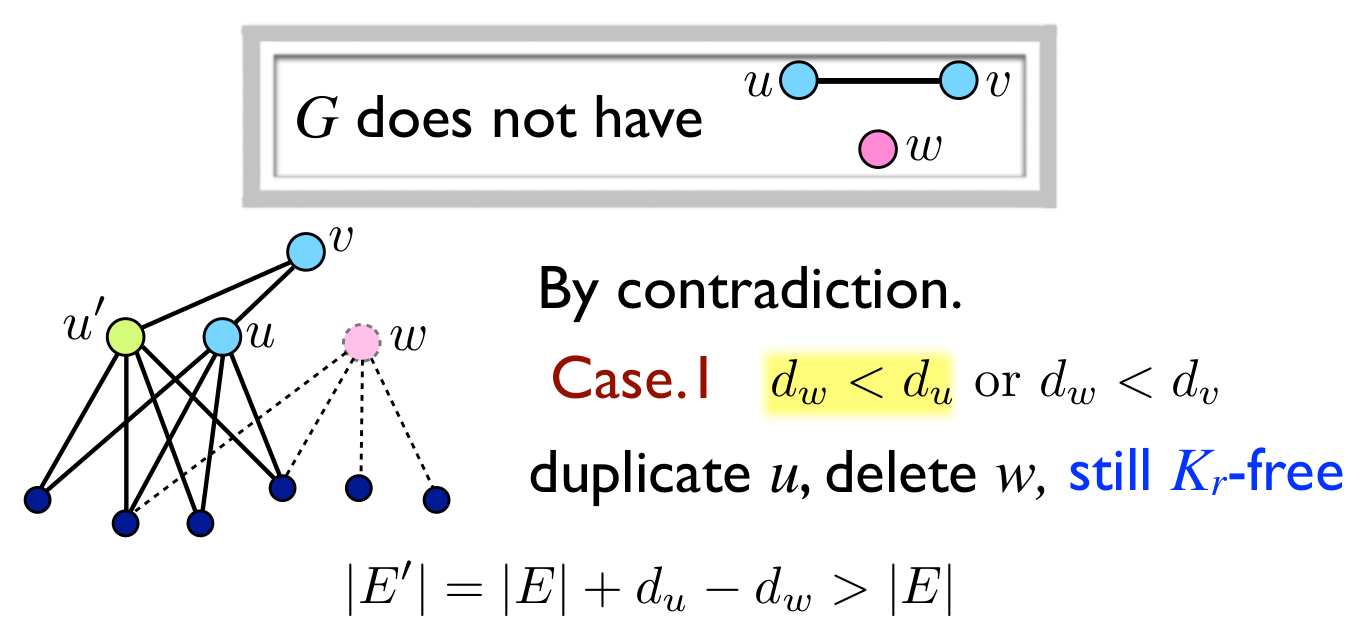
如果$G$是有最多边的$K_r$-free图, 则$G$中不存在点$u,v,w$, $uv\in E$, $uw\not\in E$, $vw\not \in E$. 数归证明如下:

$d(w)<d(u)$ 或者 $d(w)<d(v)$. 不妨设$d(w)<d(u)$, 复制$u$为$u’$, 和$u$有同样的邻居, 无边$uu’$, 去掉$w$, 则边增加了, 也没有$r$团块, 和最大矛盾.
$d(w)\ge d(u)$ 且 $d(w)\ge d(v)$. 复制$w$两次, 删掉$u$和$v$, 新图边更多且没有$r$团块, 和最大矛盾.
因此不相邻关系是等价关系, 因为$G$是完全多部图, 每个部分是一个等价类, 而因为无$r$团块, 所以至多$r-1$部分, 因此结果就是$K_{n_1,n_2,\cdots,n_{r-1}}$, 就是Turán graph.

Turán’s Theorem (independent set):

如果$G(V,E)$有$|V|=n$, $|E|=m$, 则$G$有大小$\ge n^2/(2m+n)$的独立集.
原图变成补图, 使用团块版本Turán’s Theorem.
或直接证明: 随机排列生成独立集(排在所有邻居之前), 柯西希瓦兹.

Parallel Max问题

计算$n$个不同的数中最大的
一轮比较: 至少比$\binom{n}{2}$次. 否则如果$i$和$j$没比过, 对手策略构造数据,$i$和$j$都比所有比过的大.
两轮比较: 分成$k$组, 每组$n/k$个数, 第一轮比出每组的最大值, 第二轮比$k$个最大值中的最大值, 总共$k\binom{n/k}{2}+\binom{k}{2}=O(n^{4/3})$, $k=n^{2/3}$时最优.
- 对手策略: 第一轮比了$m$次, 每次比较看做一条边, 根据Turán有$\ge \frac{n^2}{2m+n}$的点独立集, 令他们都是局部最优; 第二轮比较需要$\ge \binom{n^2/(2m+n)}{2}$次比较, 所以总共比较数量$\ge m+\binom{n^2/(2m+n)}{2}$次, 所以已经是最优的了.

2 Fobidden Cycles

围长(girth)$g(G)$: 图$G$中最小长度的环的长度.

定理

$G(V,E)$是$n$点图, 如果$g(G)\ge 5$, 那么$|E|\le \frac{1}{2}n\sqrt {n-1}$
证明:
假设$g(G)\ge 5$. 令$v_1,v_2,\cdots,v_d$为$u$的所有邻居, $d=d(u)$. 令$S_i=\{v\in V|v\sim v_i\land v\ne u\}$为$v_i$的非$u$邻居.

对于任意$v_i, v_j$, 因为$G$没有三角形, 所以$v_iv_j\not\in E$.
因为$G$中无$C_4$, 所以除了$u$以外的点都不能同时和$v_1,v_2,\cdots, v_n$中的超过1个点相邻. 因此对于$i\ne j$, $S_i\cap S_j=\emptyset$.
因此对于$\{u,v_1,v_2,\cdots,v_d\}\cup S_1\cup S_2\cup \cdots\cup S_d\subseteq V$, 有 $(d+1)+|S_1|+|S_2|+\cdots|S_d|=(d+1)+(d(v_1)-1)+(d(v_2)-1)+\cdots+(d(v_d)-1)\le n$ 因此 $\sum_{v:v\sim u}d(v)\le n-1$ 根据柯西希瓦兹定理: $n(n-1)\ge \sum_{u\in V}\sum_{v:v\sim u}d(v)=\sum_{v\in V}d(v)^2\ge \frac{\sum_{v\in V}d(v)}{n}=\frac{|E|}{n}$

3 Erdős–Stone theorem

固定一个图$H$, ex(n, H)表示满足$G\not\supseteq H$的图的最大的边数.
也就是Turán’s theorem可以写成

$ex(n,K_r)\le \frac{r-2}{2(r-1)}n^2$

极值图论基本定理 (Erdős–Stone 1946)

$K_s^r=K_{s,s,\cdots,s}$, 是$r$部图, 每部分$r$个点. 对于任意整数$r\ge 2$, $s\ge 1$, 和$\epsilon >0$, 如果$n$足够大, 每个有$n$个点和至少$(\frac{r-2}{2(r-1)}+\epsilon)n^2$条边的图中, 都包含$K_{r,s}$作为子图. 也就是

$ex(m,K_s^r)=(\frac{r-2}{2(r-1)}+o(1))n^2$

证明很复杂.

推论:

定义$ex(n,H)/\binom{n}{2}$为子图$H$的极值密度. 对于任意非空图$H$,

$\lim_{n\to \infty}\frac{ex(n,H)}{\binom{n}{2}}=\frac{\chi(H)-2}{\chi(H)-1}$

其中$\chi(H)$为$H$的染色数, 即最少的颜色数量满足点着色后相邻点都不同色.

推论证明:
令$r=\chi(H)$. 则

对于任意$n$, $H\not \subseteq T(n,r-1)$, 即$ex(n,H)\ge |T(n,r-1)|$
对于足够大的$s$, 有$H\subseteq K_s^r$, 即$ex(n,H)\le ex(n,K_s^r)$(想要有子图$K_s^r$, 一定有子图$H$)
所以 $\frac{r-2}{r-1}-o(1)\le \frac{|T(n,r-1)|}{\binom{n}{2}}\le \frac{ex(n,H)}{\binom{n}{2}}\le \frac{ex(n,K_s^r)}{\binom{n}{2}}\le \frac{r-2}{r-1}+o(1)$