The Primal-Dual Schema

1 对偶线性规划

例子

dual1

dual2

一般形式

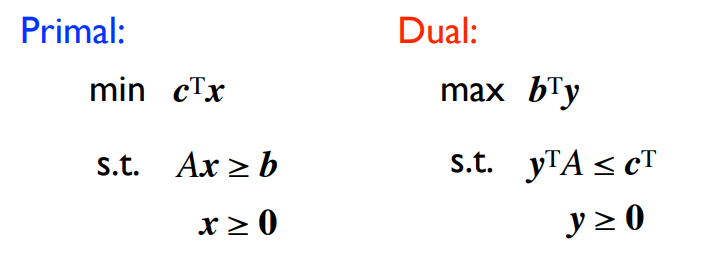
dual3

弱对偶性

任意可行解$x$和对偶解$y$, 有

$y^\top b\le c^\top x$

证明:

$y^\top b\le y^\top Ax\le c^\top x$

强对偶性

原LP问题有有限最优解$x^{*}$当且仅当对偶问题有有限最优解$y^{*}$, 且

$y^{*\top}b=c^\top x^*$

Complementary Slackness Conditions:

CSC1

Relaxed version:

CSC2

The Primal-Dual Schema

pds

2 点覆盖

算法: 找极大匹配M; 返回$C=\{v:uv\in M\}$
maximality: $C$ is a vertex cover
matching: $|M|\le OPT_{VC}$(弱对偶性)
$|C|=2|M|\le 2OPT$

对偶性

点覆盖:
限制: $\sum_{v\in e}x_v\ge 1$, 变量: $x_v\in \{0,1\}$, 最小化: $\sum_v x_v$
匹配:
变量: $\sum_{e\owns v}y_e\le 1$, 限制: $y_e\in \{0,1\}$, 最大化$\sum_e y_e$
线性规划:
prime:

$\begin{aligned} \text{minimize} &&& \sum_{v\in V}x_v\\ \text{subject to} &&&\sum_{v\in e} x_v\ge 1, &\forall e\in E\\ &&& x_v \ge 0, &\forall v\in V \end{aligned}$

dual:

$\begin{aligned} \text{maximize} &&& \sum_{e\in E}y_e\\ \text{subject to} &&&\sum_{e\owns v} y_e\le 1, &\forall v\in V\\ &&& y_e \ge 0, &\forall e\in E \end{aligned}$

在对偶线性规划中, 寻找可行解$(x,y)$满足:

$\begin{aligned} &\forall e:y_e>0==>\sum_{v\in e}x_v\le \alpha\\ &\forall v:x_v=1==>\sum_{e\owns v}y_e=1\\ \end{aligned}$

因此算法如下:

初始 $x=0,y=0$;
while $E\neq\emptyset$
$\qquad$选择$e\in E$, 将$y_e$提升到1(直到某些$v$的条件是紧的);
$\qquad$对于所有$v\in e$(紧的$v$)设置$x_v=1$, $E$中去掉所有$e\owns v$

根据这个算法, 所有删掉的$e$一定连接一个满足$x_v=1$的$v$, 且最后所有边删除了, 所以$\forall e\in E:\sum_{v\in e}x_v\ge 1$, 因此$x$是可行解.
又因为$v$是紧的, 所以$\sum_{e\owns v}y_e=1$, $y$也是可行解.

又因为

$\begin{aligned} &\forall e:\text{either }y_e=0\text{ or }\sum_{v\in e}x_v\le 2\\ &\forall v:\text{either }x_v=0\text{ or }\sum_{e\owns v}y_e=1\\ \end{aligned}$

根据relaxed complementary slackness有

$\sum_{v\in V}x_v\le 2OPT$

近似比为2.

3 Facility Location

问题

实例: 设施集合$F$, 客户集合$C$, 设施开设消耗$f:F\to [0,\infty]$, 连接消耗$c:F\times C\to [0,\infty)$
找到开放设施的子集$I\subseteq F$和连接所有客户到开放设施的路径$\phi: c\to I$
最小化总消耗$\sum_{j\in C}c_{\phi(j),j}+\sum_{i\in I} f_i$

是NP难的, 因为 set cover 可以规约到 facility location

metric facility location

连接消耗改为$d:F\times C\to [0,\infty)$, 为距离(满足对称, 非负, 三角不等式)

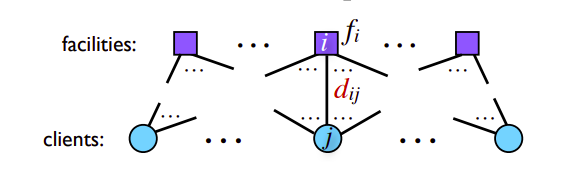
facility_location

整数线性规划

Primal

$\begin{aligned} \text{minimize} &&& \sum_{i\in F, j\in C}d_{ij}x_{ij}+\sum_{i\in F}f_iy_i\\ \text{subject to} &&& y_i- x_{ij}\ge 0 && \forall i\in F,j\in C\\ &&& \sum_{i\in F}x_{ij}\ge 1 && \forall j\in C\\ &&& x_{ij}, y_i\in \{0,1\} &&\forall i\in F,j\in C \end{aligned}$

relaxation: 最后一个条件改为$x_{ij},y_i\ge 0$

Dual-relax

$\begin{aligned} \text{maximize} &&& \sum_{j\in C}\alpha_j\\ \text{subject to} &&& \alpha_j-\beta_{ij}\le d_{ij} && \forall i\in F, j\in C\\ &&& \sum_{j\in C}\beta_{ij}\le f_i, &&\forall i\in F\\ &&&\alpha_j, \beta_{ij}\ge 0 &&\forall i\in F,j\in C \end{aligned}$

$\alpha_j$: 客户$j$为所有设施付出的钱
$\beta_{ij}\ge \alpha_j-d_{ij}$: 客户$j$付给设施$i$的钱(减去$j$到$i$的过路费后)
目标: 收最多的钱, 一家医院都不开

complimentary slackness conditions(理想情况):

$ x_{ij}=1\to a_j-\beta_{ij}=d_{ij}$
$y_i=1\to \sum_{j\in C}\beta_{ij}=f_i$
$\alpha_j>0\to \sum_{i\in F}x_{ij}=1$
$\beta_{ij}>0\to y_i=x_{ij}$

算法

根据上面complimentary slackness conditions的1和2得到算法:

初始$\alpha=0,\beta=0$, 没有客户连接, 没有设施开放;
按照一个均匀连续的速率, 同时提升所有客户的$a_j$的值
- 对于关闭的设施$i$, 一旦$a_j=d_{ij}$, 边$(i,j)$就被买通了, 固定$\beta_{ij}=\alpha_j-d_{ij}$
- 一旦$\sum_{j\in C}\beta_{ij}=f_i$, 暂时开放设施$i$, 所有满足(还未被连接, 但是买通了边$(i,j)$ )的客户$j$, 都被连接到设施$i$, 停止提升$a_j$($j$已经可以被服务).
- 对于还没被连接的客户$j$和已经开放的设施$i$, 一旦$a_j=d_{ij}$, 客户$j$就连接到设施$i$, 停止提升$a_j$(不称为买通(paid))
分析:
- 如果事件同时发生, 按照随机顺序处理
- 买满了的设施假设开放: $\sum_{j\in C}\beta_{ij}=f_i$
- 每个客户通过一条紧的边($\alpha_{j}-\beta_{ij}=d_{ij}$)连接到开放的设施
- 最终所有客户都连接到假设开放的设施
- 一个客户可能有多条紧的边, 所以连接到了多个设施; 我们可能已经开放了不必要的设施.
改进:
- 将上面的步骤作为阶段1
- 增加阶段2:
  - 构建图$G(V,E)$, $V$={暂时开放的设施}, $(i_1,i_2)\in E$ 当且仅当存在客户$j$, 满足$(i_1,j)$和$(i_2,j)$都在阶段1被买通.
  - 找到$G$的极大独立集$I$, 永久开放
- 得到的解不确保服务所有人
- 在metric facility location问题中, 对于没有被服务到的人, 最多沿着沿着被买通的边走三次, 就能走到别的医院(间接连接到开放的设施), 也就服务到了所有人.
近似比分析:
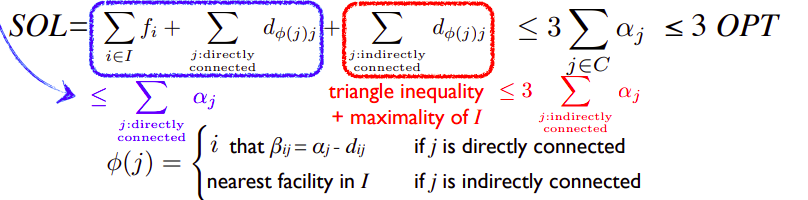
算法可以离散地执行, 时间复杂度$O(m\log m)$, $m=|F||C|$